Здесь Вы можете оставлять свои комментарии к статьям. Все статьи

- 19.03.2024 Весенняя распродажа!
- 22.02.2024 С Днем защитника Отечества!
20 августа в 11:00 МСК состоится вебинар по теме "Объектовое оборудование: УОО "Протон-16"
Подключиться к трансляции можно по ссылке https://youtu.be/qJgab9miEkE
Часто задаваемые вопросы и ответы по системе «Радиус», «Протон», «Автограф»
Пресс-центр

ФУНКЦИОНАЛЬНЫЕ ВОМОЖНОСТИ АСИНХРОННО-АДРЕСНЫХ РАДИООХРАННЫХ СИСТЕМ
В 2004 году в НПО «Центр-Протон» была выполнена научно-исследовательская работа «Оптимизация параметров конфигурации асинхронно-адресных РСПИ», наиболее важные результаты которой были изложены в [1] применительно к радиоохранным системам. Самыми фундаментальными были выводы о зависимости оптимального количества bопт повторов сообщений от допускаемой вероятности Рни неприема сообщений в часы пик и о существовании оптимальной занятости радиоканала G = 0.35 в часы пик, обеспечивающей охрану наибольшего количества объектов.
В настоящей работе детализируется ряд вопросов, затронутых в [1] и [2], с учетом практического опыта эксплуатации РСПИ.
Одним из самых важных является вопрос о выборе допустимой вероятности Рни неприема сообщений в часы пик. Из физических соображений ясно, что выбор Рни является компромиссом между надежностью доставки сообщений от охраняемых объектов и максимальным количеством охраняемых объектов на одной выделенной частоте. Такой компромисс является типичным для РСПИ, развернутых в крупных населенных пунктах, с большим количеством абонентов.
При выборе Рни необходимо учитывать ряд факторов, характерных для эксплуатации охранных РСПИ:
- Подавляющая часть передаваемых в системах сообщений являются служебными (~99%).
- Относительная доля тревожных сообщений невелика (~1%).
- Большая часть передаваемых тревожных сообщений является ложными тревогами, вызванными неправильными действиями абонентов и неисправностями объектового оборудования.
- Относительная доля «боевых» тревог в общем количестве тревожных сообщений невелика (порядка 10–20%).
- Подавляющая часть «боевых» тревог приходится на время вне часов пик, а их относительная доля от общего количества сообщений не превышает (0,1 – 0,2)%.
Главной задачей охранных РСПИ является надежная доставка прежде всего «боевых» тревожных сообщений. Вероятность неприема этих сообщений вне часов пик резко падает, причем чем больше количество повторов bтр тревожных сообщений, тем ниже вероятность неприема.
С учетом изложенного можно предположить, что в тех случаях, когда основным требованием является надежная доставка любого сообщения, в качестве типичной величины вероятности неприема сообщений Рни в часы пик может быть принята Рни≤10-3 , что примерно соответствует среднесуточному коэффициенту потерь сообщений не более 10-4.
В некоторых случаях, когда стоит задача охраны наибольшего количества объектов ценой потери части служебных сообщений, вероятность Рни может быть принята достаточно большой, порядка 0,01…0,03. Экономически это может оказаться оправданным, что подтверждается практикой эксплуатации екатеринбургской радиосистемы ОКО-1, где допускается среднесуточный коэффициент потерь сообщений ~0,003, что примерно соответствует вероятности неприема сообщений в часы пик порядка 0,03.
Очень эффективным способом дополнительного уменьшения вероятности неприема тревожных сообщений является повышение количества повторов bтр для этой категории сообщений. Общая занятость радиоканала при этом возрастает не более чем на 1%, что можно считать практически несущественным. Например: в РСПИ «Протон» производства НПО «Центр-Протон» принята вероятность неприема служебных сообщений в часы пик Рни=10-3. Оптимальное количество повторов служебных сообщений bсл=10 . Для передачи тревожных сообщений количество повторов увеличено до bтр=16 .
Вторым по значимости является вопрос выбора оптимального количества повторов служебных сообщений. Рассмотрим его подробно.
В [1] была получена формула (6), связывающая максимальную частоту ![]() суммарного потока сообщений в часы пик с заданными Рни и b:
суммарного потока сообщений в часы пик с заданными Рни и b:
|
|
(1) |
где tc – длительность одной посылки, передающей сообщение.
Умножив обе части (1) на tc , получим соответствующую максимальную занятость радиоканала ![]() при заданных Рни и b:
при заданных Рни и b:
| |
(2) |
Введем понятие эффективной занятости GЭ:
| |
(3) |
Физический смысл GЭ – это исходная занятость радиоканала, которую формирует поток первичных (без повторных) сообщений от охраняемых объектов. Именно GЭ характеризует эффективность использования пропускной способности радиоканала и, в конечном счете, максимальное количество объектов, которое можно эксплуатировать в РСПИ при заданных Рни и b. В частном случае, при ![]() , GЭ достигает максимального значения
, GЭ достигает максимального значения ![]() :
:
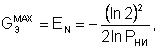 |
(4) |
где EN – оптимальный коэффициент эффективности системы по количеству охраняемых объектов (формула (13) в [1]).
Представляет интерес детальный характер зависимостей Gэ от количества повторов b при разных допустимых Рни. Графики этих зависимостей приведены на рис.1. Из графиков видно, что при каждой заданной Рни существует максимальное значение ![]() при соответствующем оптимальном количестве повторов bопт, причем сами максимумы не острые. Необходимо отметить, что расчетные значения bоп в общем случае нецелочисленны, и их нужно округлять до ближайших целочисленных значений.
при соответствующем оптимальном количестве повторов bопт, причем сами максимумы не острые. Необходимо отметить, что расчетные значения bоп в общем случае нецелочисленны, и их нужно округлять до ближайших целочисленных значений.
Введем понятие коэффициента эффективности Кэ использования повторов сообщений как отношение ![]() к
к ![]() при заданном значении в часы пик:
при заданном значении в часы пик:
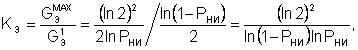 |
(5) |
где ![]() – эффективная занятость радиоканала для заданной вероятности Рни в случае b = 1, т.е. при отсутствии повторов сообщений. В таблице 1 приведены результаты расчетов зависимостей bопт ,
– эффективная занятость радиоканала для заданной вероятности Рни в случае b = 1, т.е. при отсутствии повторов сообщений. В таблице 1 приведены результаты расчетов зависимостей bопт , ![]() и Кэ от заданной вероятности Рни .
и Кэ от заданной вероятности Рни .
Таблица 1
| Рни | 10-6 | 10-5 | 10-4 | 10-3 | 10-2 | 10-2 | 10-1 |
| bопт |
19,93 |
16,61 |
13,29 |
9,97 |
6,65 |
5,05 |
3,32 |
| |
0,0175 |
0,021 |
0,026 |
0,035 |
0,052 |
0,068 |
0,104 |
| Кэ |
34800 |
4170 |
522 |
69,5 |
10,4 |
4,49 |
1,98 |
Из рис.1 и табл.1 видна высокая эффективность применения повторов сообщений при малых допустимых вероятностях Рни и очень низкая – при высоких значениях Рни .
Для упрощения последующего анализа покажем, что все кривые зависимостей Gэ от b подобны по форме независимо от заданной Рни . Для этого введем понятия нормированных значений ![]() и
и ![]() . После соответствующих подстановок в (3), опуская промежуточные преобразования, приведем формулу, связывающую Gn и bn:
. После соответствующих подстановок в (3), опуская промежуточные преобразования, приведем формулу, связывающую Gn и bn:
| |
(6) |
Полученная расчетная зависимость (не являющаяся функцией Рни ) отражена в таблице 2.
Таблица 2
| bn |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
| Gn |
0,014 |
0,229 |
0,502 |
0,702 |
0,830 |
0,910 |
0,958 |
0,984 |
0,997 |
|
|
|
|
|
|
|
|
|
|
|
| bn |
1,0 |
1,2 |
1,5 |
2,0 |
3,0 |
4,0 |
5,0 |
10,0 |
|
| Gn |
1,000 |
0,990 |
0,956 |
0,886 |
0,759 |
0,663 |
0,590 |
0,390 |
|
Таблица 2 позволяет определить, в какой степени отклонение b от bопт снижает Gэ.
Если допустить снижение Gэ на 10% (т.е. ![]() ), то диапазон допустимых значений b будет находиться в пределах (0,6 - 1,9)bопт. Для 20% снижения (
), то диапазон допустимых значений b будет находиться в пределах (0,6 - 1,9)bопт. Для 20% снижения (![]() ) соответствующий диапазон равен (0,5 - 2,6)bопт .
) соответствующий диапазон равен (0,5 - 2,6)bопт .
Физически это означает, что указанные сниженные значения эффективной занятости радиоканала могут быть получены как при малом количестве повторов и, соответственно, сниженной (относительно Gэ = 0,35) занятости радиоканала в часы пик, так и, наоборот, при увеличенных количестве повторов и занятости радиоканала G > Gопт. Например, для Рни = 10-3, bопт = 9,97 и ![]() = 0,035, Gmax = 9.97 · 0.035 = 0.35. Если допустить снижение эффективной занятости до
= 0,035, Gmax = 9.97 · 0.035 = 0.35. Если допустить снижение эффективной занятости до ![]() , то соответствующее количество повторов может быть снижено до 0,5 · 9,98 ≈ 5, а физическая занятость радиоканала в часы пик должна быть уменьшена до 5 · 0,028 = 0,140 . И наоборот, если допустить увеличение количества повторов до b = 2.6 · 9.97 ≈ 26 , то соответствующая занятость радиоканала должна быть повышена до 26 · 0.028 = 0.728.
, то соответствующее количество повторов может быть снижено до 0,5 · 9,98 ≈ 5, а физическая занятость радиоканала в часы пик должна быть уменьшена до 5 · 0,028 = 0,140 . И наоборот, если допустить увеличение количества повторов до b = 2.6 · 9.97 ≈ 26 , то соответствующая занятость радиоканала должна быть повышена до 26 · 0.028 = 0.728.
Покажем, что эти 2 варианта режимов, будучи равноценными по значению Gэ в часы пик, существенно отличаются по другим эксплуатационным характеристикам (вне часов пик). С учетом того, что занятость радиоканала ![]() , формулу (5) в [1] можно записать в виде:
, формулу (5) в [1] можно записать в виде:
| |
(7) |
На рис.2 представлено семейство графиков Рни(G) при разных значениях количества повторов. Из графиков видно, что при малых занятостях G радиоканала и больших значениях b вероятность неприема Рни резко снижается. Так, если для рассмотренных выше (в примере) двух режимов задать 1,5-кратное снижение занятости радиоканала, т.е. G1= 0,140/1,5 = 0,093 и G2 = 0,728/1,5 = 0,485 при соответствующих b1 = 5 и b2 = 26 , то получим следующие вероятности неприема Рни:
Рни1 = [1 - exp(-0,186)]5 = 141 · 10-6 (снижение в 7 раз) и
Рни2 = [1 - exp(-0,970)]26 = 4,2 · 10-6 (снижение в 240 раз!).
Таким образом, при равных вероятностях неприема ( Рни = 10-3) в часы пик и равных эффективных занятостях (Gэ = 0,028) эти два варианта режимов эксплуатации РСПИ весьма существенно (в 34 раза!) отличаются по вероятности неприема сообщений вне часов пик. Причем видно явное преимущество режима с повышенным количеством повторов (b ≥ bопт ). При дальнейшем снижении физической занятости радиоканала преимущество режима с повышенным количеством повторов прогрессирующе растет. Поэтому количество повторов должно выбираться не менее 10. Это позволит уменьшить (при заданной вероятности неприема Рни в часы пик) среднесуточное количество непринятых сообщений по системе в целом.
Далее покажем, что при b = 10 (оптимальном для Рни = 10-3) обеспечивается режим эксплуатации РСПИ, близкий к оптимальному, для широкого диапазона требуемых вероятностей неприема Рни в часы пик. Для этого подставим b = 10 в (3) и (2) и рассчитаем Gэ, Gmax и Gn для ряда значений Рни. Результаты расчета приведены в таблице 3.
Таблица 3
| Рни | 10-6 | 3 · 10-6 | 10-5 | 3 · 10-5 | 10-4 | 3 · 10-4 |
| Gэ |
0,0145 |
0,0165 |
0,0190 |
0,0218 |
0,0254 |
0,0294 |
| Gmax |
0,145 |
0,165 |
0,19 |
0,218 |
0,254 |
0,294 |
| Gn |
0,834 |
0,874 |
0,909 |
0,944 |
0,973 |
0,993 |
|
|
|
|
|
|
|
|
| Рни | 10-3 | 3 · 10-3 | 10-2 | 3 · 10-2 | 10-1 |
|
| Gэ |
0,0347 |
0,0410 |
0,0499 |
0,0609 |
0,0791 |
|
| Gmax |
0,347 |
0,410 |
0,499 |
0,609 |
0,791 |
|
| Gn |
1,000 |
0,993 |
0,958 |
0,889 |
0,760 |
|
Из таблицы видно, что если допустить ≈ 12% снижение эффективной занятости радиоканала, то при фиксированном значении b = 10 диапазон допустимых вероятностей Рни достигает 4 порядков (от 3 · 10-6 до 3 · 10-2 )! Соответствующая максимальная занятость радиоканала в часы пик Gmax при этом меняется от 0,165 до 0,609 (при оптимальной занятости 0,347 для Рни = 0,001).
Необходимо отметить, что понятие вероятности неприема Рни сообщений в часы пик удобно для выявления общих закономерностей функционирования РСПИ при теоретическом анализе, но ее применение в качестве практического критерия надежности доставки сообщений вызывает существенные трудности, связанные как с неопределенностью понятия часов пик, так и с невозможностью реализации алгоритма автоматического обнаружения превышения допустимой Рни. Поэтому представляется целесообразным в качестве практического критерия надежности доставки сообщений принять коэффициент среднемесячных потерь Рнс сообщений как отношение количества непринятых сообщений за месяц к общему количеству принятых за месяц сообщений. Для автоматического вычисления этого коэффициента необходима нумерация передаваемых сообщений от каждого из охраняемых объектов, как это сделано, например, в объектовом оборудовании екатеринбургской фирмы «ОКО» и челябинской фирмы «Центр-Протон». В качестве нормы этого коэффициента предлагается Рнс ≤ 10-4 (примерно соответствует Рни ≤ 10-3 ).
Указанная выше норма относится только к потерям сообщений, вызванным взаимными внутрисистемными помехами. В условиях воздействия на ЦСМ внешних, внесистемных помех этот показатель может резко возрасти. Поэтому в ЦСМ обязательно должна быть функция своевременного обнаружения внешних помех, нарушающих работу РСПИ.
В связи с рассматриваемыми вопросами невозможно оставить без внимания публикацию В.Белкина [2]. В статье рассматривается та же задача, что и в [1], но с более общих позиций, с учетом соотношения h уровней сигнала и шума. В принципе, такой анализ кажется вполне уместным, если бы не одно обстоятельство: в силу нестабильности условий распространения радиоволн РСПИ никогда не эксплуатируются с предельно малыми соотношениями сигнал-шум. Реально это отношение всегда больше 7 и вероятность неприема Pb → 0 . Следовательно, вероятность неприема сообщения Pr практически будет определяться только эффектом наложения сигналов во времени, т.е. ![]() .
.
Далее, как следует из принятого автором равновероятного на интервале наблюдения Тнабл момента выхода на связь в часы пик каждого из N объектов системы, суммарный поток сообщений является простейшим, т.е. пуассоновским. Для анализа же пуассоновских потоков существует наработанный математический аппарат, примененный в [1] и позволивший получить выводы, имеющие фундаментальный характер.
Анализ структуры формулы для расчета Pа в [2] позволяет сделать вывод, что автор в расчете Pа применил распределение, известное в теории вероятностей как биномиальное. Такой подход вполне правомерен и при корректном применении дает достоверные результаты, которые должны совпасть с результатами анализа в [1]. Действительно, при выполнении условия 2Тк/ Тнаблr в [2] должны быть одинаковыми. Однако, первые же оценочные расчеты показали очень большие расхождения:
Рис.1: Кривая Pr для r = 10, h = 30. Pr ≈ 4 · 10-9. Расчет Рни для этого же случая по [1] дает: G = N · r · Тк/ Тнабл = 2,778 и Рни = [1 - exp(-2 · 0,2778)]10 = 2 · 10-4 . Результаты различаются в 50000 раз!
Рис.4: Экстремум кривой Pr для N = 1000, r = 15 дает Pr = 1,8 · 10-9. Расчет Рни для этого же случая по [1] дает: G = N · r · Тк/ Тнабл = 0,4167 и Рни = [1 - exp(-2 · 0,4167)]15 = 1,93 · 10-4 . Результаты различаются в 100000 раз!
Рис.2: Кривая Pr для N = 10, h = 7. Pr = 2,7 · 10-7 . Расчет Рни по [1] дает: G = N · r · Тк/ Тнабл = 2,778 · 10-4 и Рни = [1 - exp(-2 · 0,0002778)]1 = 5,55 · 10-4 . Разница в 2000 раз! Кроме того, двойной в логарифмическом масштабе наклон кривой с параметром h = 7 противоречит физической сути процессов при малых занятостях радиоканала. Должен быть одиночный наклон.
Столь большие расхождения вынуждают предположить наличие какой-то грубой ошибки в [2]. И такая ошибка была обнаружена: в формуле для расчета Ра в значке Σ вместо нижнего предела i = 1 ошибочно стоит i = 2. Это противоречит физическому смыслу процесса приема сообщения в условиях мешающего действия аналогичных сообщений от других объектов. Для неприема рассматриваемого сообщения необходимо попадание на интервал 2Тк хотя бы одного мешающего сообщения, т.е. суммирование вероятностей должно вестись, начиная с i = 1 и до i = (N - 1) · r .После устранения ошибки в формуле для расчета Ра в [2] результаты расчета Pr при h ≥ 7 практически совпали с результатами расчета Рни в [1].
Действительно, Pa = (1 - Po) , где Po – вероятность противоположного события – приема одиночного события, состоящего в том, что на интервал времени 2Тк не попадет ни одного мешающего сообщения. Но ![]()
![]() и Рни = [1 - exp(-2G)] , где G = Тк · S/Тнабл – занятость радиоканала. Тогда Pа= Pно – вероятность неприема одиночного сообщения в [1], что и требовалось доказать.
и Рни = [1 - exp(-2G)] , где G = Тк · S/Тнабл – занятость радиоканала. Тогда Pа= Pно – вероятность неприема одиночного сообщения в [1], что и требовалось доказать.
В итоге, приведенные в [2] графики зависимостей на рис.1 – рис.4 следует признать недостоверными, а выводы – лишенными той общности, которая была характерна для [1]. Следующими по важности является вопрос о величине времени доставки Тд сообщения. Из физических соображений ясно, что можно говорить только о средневероятностном времени доставки сообщений ![]() , причем это время должно быть пропорционально среднему значению межпосылочного интервала времени
, причем это время должно быть пропорционально среднему значению межпосылочного интервала времени ![]() и зависеть от занятости радиоканала
и зависеть от занятости радиоканала ![]() . В частности, при малых занятостях (вне часов пик) наиболее вероятен прием уже первой посылки. С увеличением занятости радиоканала должно монотонно возрастать, достигая наибольшего значения при максимальной занятости, характерной для часов пик.
. В частности, при малых занятостях (вне часов пик) наиболее вероятен прием уже первой посылки. С увеличением занятости радиоканала должно монотонно возрастать, достигая наибольшего значения при максимальной занятости, характерной для часов пик.
Приведем без вывода формулу для расчета ![]() :
:
| |
(8) |
где exp(-2G) – вероятность приема одиночного сообщения.
В таблице 4 приведена зависимость нормированного средневероятностного времени доставки сообщения ![]() от занятости радиоканала G для фиксированного количества повторов b = 10.
от занятости радиоканала G для фиксированного количества повторов b = 10.
Таблица 4
| G |
0,050 |
0,100 |
0,165 |
0,250 |
0,347 |
0,500 |
0,609 |
1,00 |
| |
0,105 |
0,221 |
0,391 |
0,653 |
0,990 |
1,600 |
2,010 |
2,560 |
Из таблицы 4 видно, что при оптимальной занятости радиоканала Gопт = 0,347 в часы пик ![]() не превышает одного значения межпосылочного интервала времени
не превышает одного значения межпосылочного интервала времени ![]() , монотонно снижаясь по мере снижения занятости вне часов пик.
, монотонно снижаясь по мере снижения занятости вне часов пик.
Необходимо отметить, что в связи с вероятностным характером процессов приема сообщений, наибольшее время доставки сообщений равно ![]() с вероятностью доставки Pд = (1 - Рни). Это время не должно превышать нормативного
с вероятностью доставки Pд = (1 - Рни). Это время не должно превышать нормативного ![]() . В качестве нормативного предлагается принять 1 минуту.
. В качестве нормативного предлагается принять 1 минуту.
Для исключения детерминированного наложения во времени посылок от разных объектов, Тмп должен формироваться по случайному закону с диапазоном рассеивания ![]() , в (10…20) раз превышающим длительность tc одиночной посылки, передающей сообщение.
, в (10…20) раз превышающим длительность tc одиночной посылки, передающей сообщение.
Практически приемлемыми являются следующие параметры: ![]() ,
, ![]() , закон распределения Тмп – равновероятный на интервале от
, закон распределения Тмп – равновероятный на интервале от ![]() до
до ![]() с постоянной плотностью вероятности 1 / ΔТмп. Допускается равновероятно-дискретное распределение с количеством дискрет не менее 8 на интервале рассеивания ΔТмп . При выполнении этих условий суммарный поток сообщений в эфире будет близок к пуассоновскому из-за одновременного суммирования большого количества независимых случайных потоков сообщений от разных объектов. Это повышает надежность оценок вероятностных характеристик РСПИ.
с постоянной плотностью вероятности 1 / ΔТмп. Допускается равновероятно-дискретное распределение с количеством дискрет не менее 8 на интервале рассеивания ΔТмп . При выполнении этих условий суммарный поток сообщений в эфире будет близок к пуассоновскому из-за одновременного суммирования большого количества независимых случайных потоков сообщений от разных объектов. Это повышает надежность оценок вероятностных характеристик РСПИ.
В результате проведенного анализа можно сделать следующие выводы:
1. В качестве практически оптимального количества повторов служебных сообщений для широкого диапазона вероятностей Рнс рекомендуется принять bсл= 10, а для тревожных сообщений – bтр= 16 .
2. В качестве нормы среднемесячной вероятности недоставки сообщений Рнс по РСПИ в целом, вызванной внутрисистемными помехами, предлагается принять Рнс ≤ 10-4, а в экономически обоснованных случаях – Рнс ≤ 10-3 . Для реализации функции автоматического определения Рнс в РСПИ должна быть нумерация передаваемых объектами сообщений.
3. Для повышения надежности работы РСПИ в ЦСМ необходима функция автоматического обнаружения внешних, внесистемных помех.
4. Межпосылочный интервал времени при передаче сообщений от объектов должен быть модулирован по случайному закону.
5. В процессе разворачивания РСПИ (роста количества охраняемых объектов N) Рнс прогрессирующе растет. При некотором предельном Nmax будет достигнута предельно допустимая вероятность Рнс , после чего дальнейшее наращивание количества объектов будет возможным только на дополнительно выделенных рабочих частотах.
ЛИТЕРАТУРА
- Зуев П. Вероятностный анализ функциональных возможностей асинхронно-адресных радиоохранных систем // Алгоритм безопасности. – 2004, №2.
– с 52 – 55. URL: http://www.algoritm.org/arch/04_2/04_2_19.pdf (дата обращения 7.06.11) - Белкин В. Вероятность доставки сообщений в радиосистемах передачи извещений асинхронно-адресного типа // Алгоритм безопасности. – 2006, №2.
– с 60 – 62. URL: http://www.algoritm.org/arch/06_2/06_2_17.pdf (дата обращения 7.06.11)
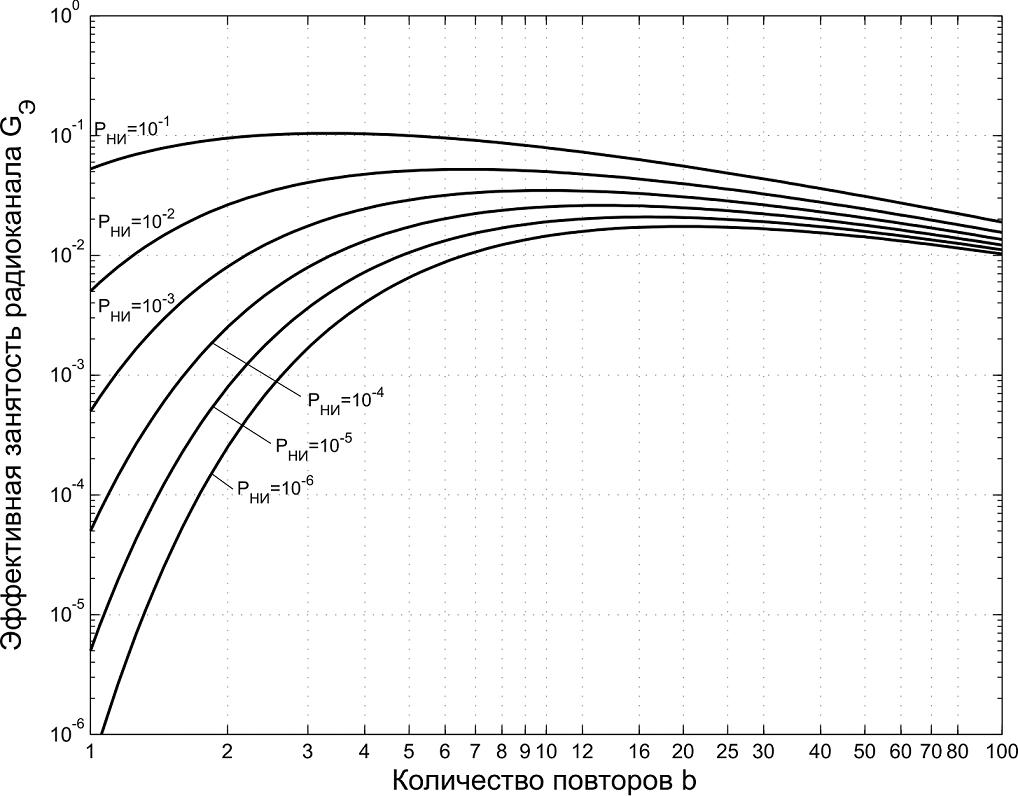
Рисунок 1
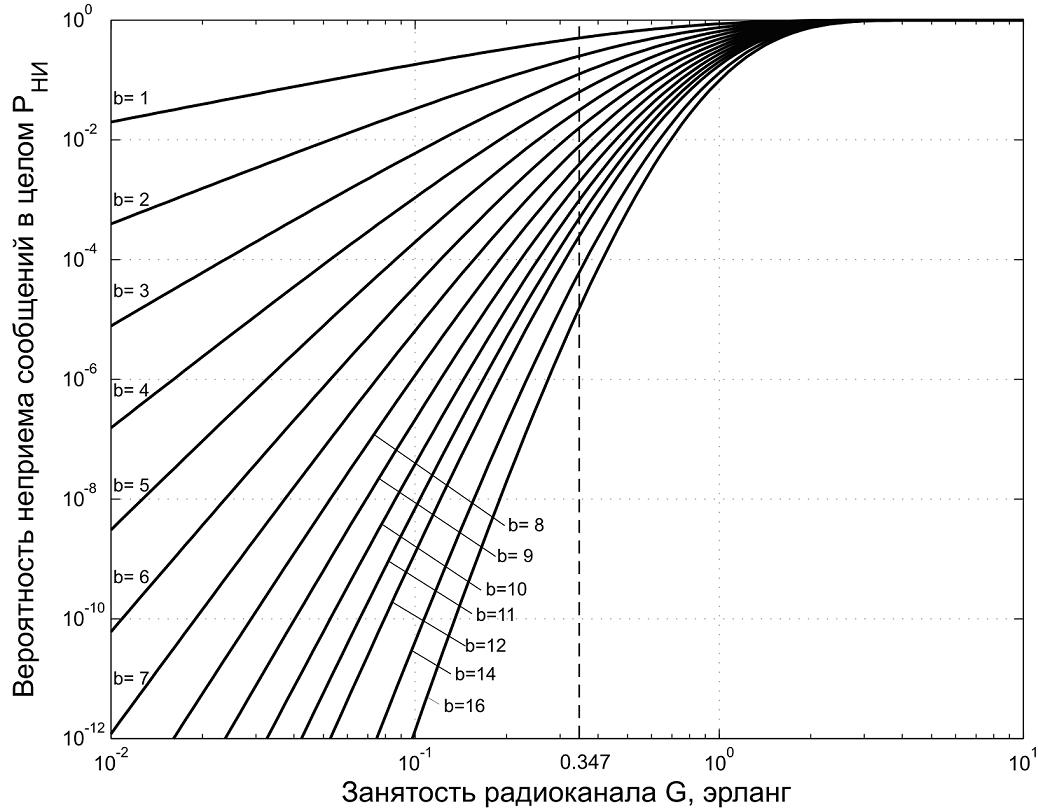
Рисунок 2

Алтай Республика
Алтайский край
Амурская область
Архангельская область
Астраханская область
Башкортостан
Белгородская область
Брянская область
Бурятия республика
Владимирская область
Волгоградская область
Вологодская область
Воронежская область
Дагестан
Еврейский АО
Забайкальский край
Ивановская область
Ингушетия Республика
Иркутская область
Кабардино-Балкария
Казахстан
Калининградская область
Калмыкия
Калужская область
Камчатский край
Карачаево-Черкессия Республика
Карелия
Кемеровская область
Кировская область
Корякский АО
Костромская область
Краснодарский край
Красноярский край
Крым Республика
Курганская область
Курская область
Ленинградская область
Липецкая область
Магаданская область
Марий Эл республика
Молдова
Мордовия Республика
Москва
Московская область
Мурманская область
Ненецкий АО
Нижегородская область
Новгородская область
Новосибирская область
Омская область
Оренбургская область
Орловская область
Пензенская область
Пермский край
Приморский край
Псковская область
Ростовская область
Рязанская область
Самарская область
Саратовская область
Саха Республика (Якутия)
Сахалинская область
Свердловская область
Севастополь
Северная Осетия-Алания Республика
Смоленская область
Ставропольский Край
Таймырский АО
Тамбовская область
Татарстан Республика
Тверская область
Томская область
Тульская область
Тыва, республика
Тюменская область
Удмуртская республика
Ульяновская область
Хабаровский край
Хакасия
Ханты-Мансийский АО
Челябинская область
Чеченская республика
Читинская область
Чувашская республика
Чукотский АО
Эвенский АО
Ямало-Ненецкий АО
Ярославская область